Matrix Mnemonics

Reading matrix notation is burdened by the trivial things like rows being indexed before columns. An author can be trying to communicate something simple, yet the reader's cognitive load can be high as they unpack the matrix notation.

Here, I'm experimenting with ways to make matrix notation more memorable.

Indexing

There is no fundamental reason why rows should appear before columns in matrix indexing. It's just a convention to be remembered.

History of indexing

Where did the indexing convention come from? Below I mention two notes taken from an article by John Aldrich, Earliest Uses of Symbols for Matrices and Vectors.

In the very first pages of Thomas Muir's The Theory of Determinants in Historical Order of Development by Thomas Muir we see a letter written by Leibnitz to L'Hospital in April 1698 explaining his notation:

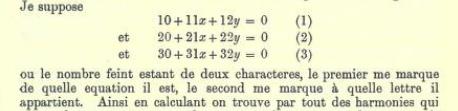
Here he mentions that the first number represents the equation and the second number represents the member terms of that equation. A scanned copy of the book is freely available on the Internet Archive.

By the 1800's we see notation very similar to our modern expectations. The following appears in 1815 in writing by Cauchy, again the context is that of systems of equations:

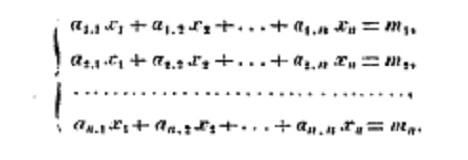
With rows of equations, it seems natural to refer first to the equation and then the element within. So, even if linear algebra and the use of matrices has evolved far beyond systems of equations, knowing this piece of history can help you recall the indexing order of matrices.

Multiplication

For matrix multiplication, it can be difficult to remember the details of how the two matrices interact, and what the meaning of this interaction is. My preference is to view matrix multiplication as repeatedly mixing together a list of inputs. I wrote a separate post describing this conceptualization in more detail: Visualizing Matrix Multiplication.

Multiplication semantics

In an expression like \( \matr{A}\matr{B} = \matr{C} \) where \( \matr{A} \), \( \matr{B} \) and \( \matr{C} \) are matrices, one can often view the expression as representing either:

1. \( \matr{A} \) mixes the rows of \( B \) to produce rows in \( C \), or
2. \( \matr{B} \) mixes the columns of \( A \) to produce columns in \( C \).

The following is a verse to help remember this duality and the order:

In both #1 and #2 above, we have one of the matrices acting as list of input objects and the other matrix mixing the inputs together multiple times. We can express this without any mention of rows and columns and get closer to the heart of matrix multiplication:

When you come across a matrix multiplication, it's useful to spend a moment to see this mixing of objects interpretation is useful. To do so, a good sequence in which to try and assign roles to the rows and columns of the 2 matrices involved is suggested below.

If these last three mnemonics don't seem to make much sense, check the page Visualizing Matrix Multiplication for a more detailed explanation.