\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \newcommand{\E} {\mathrm{E}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \newcommand{\groupMul}[1] { \cdot_{\small{#1}}} \newcommand{\inv}[1] {#1^{-1} } \)
Math and science::Algebra::Aluffi

Monomorphisms and epimorphisms

The ideas of injections and surjections in the context of sets and functions is paralleled in the context of categories by the concepts of monomorphisms and epimorphisms.

Monomorphism

Let \( \cat{C} \) be a category and \( A \) and \( B \) be objects of \( \cat{C} \). A morphism \( f \in \cathom{C}(A, B) \) is said to be a monomophism iff:

For all objects \( Z \) of \( \cat{C} \) and all morphisms \( \alpha', \, \alpha'' \in \) \( \cathom{C}(Z, A) \)

\[f \, \alpha' = f \, \alpha'' \implies \alpha' = \alpha''. \]

An epimorphism is defined similarly, but with the composition order reversed.

Epimorphism

Let \( \cat{C} \) be a category and \( A \) and \( B \) be objects of \( \cat{C} \). A morphism \( g \in \cathom{C}(A, B) \) is said to be a monomophism iff:

For all objects \( Z \) of \( \cat{C} \) and all morphisms \( \beta', \, \beta'' \in \) \( \cathom{C}(B, Z) \)

\[\beta' \, g =  \beta'' \, g \implies \beta' = \beta''. \]

Essense

If \( f \) is a monomorphism and \( f \, \alpha \) is \( f \) composed with some unknown morphism \( \alpha \), then knowing \( f \) and \( f \, \alpha \) is enough to information to recover \( \alpha \) exactly.

In other words, there is no redundancy prodived by \( f \) that allows two morphisms \( \alpha' \) and \( \alpha'' \) to compose with \( f \) such that \( f \, \alpha' \) and \( f \, \alpha'' \) produce the same morphism.

Yet another wording: no morphism can 'hide' behind \( f \).

Similarly, an epimorphism \( g \) does not afford any ambiguity to morphisms that compose after \( g \).


\( \lnot \) (monomorphic \( \land \) ephimorphic \( \iff \) isomorphic)

Functions between sets are injective iff they are monomorphisms, and they are surjective iff they are epimorphisms. Consequently, a function is isomorphic iff it is monomorphic and epimorphic.

This bi-implication relationship, (monomorphic ∧ epimorphic ⇔ isomorphic), is true for the category \( \mathrm{Set} \), but it is not true for categories in general. For example, the category formed by the relation ≤ on the inteters: all morphisms are both monomorphisms and epimorphisms, but only a subset of morphisms, the identies, are isomorphisms.

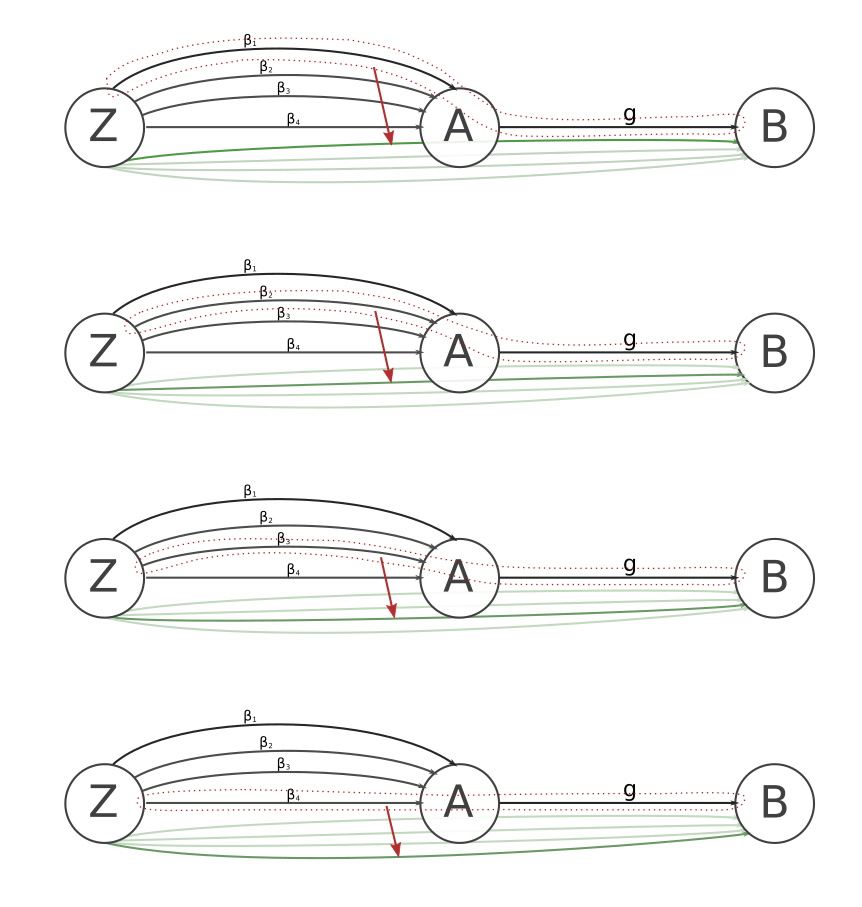
Injective relationship between morphisms

The following diagram tries to hint at the idea that a monomorphism \( g \) induces an injective map forming composition morphisms when \( g \) is the second morphism. An analagous situation describes an epimorphism inducing an injection when the epimorphism is applied first in a composition.

Source

p29