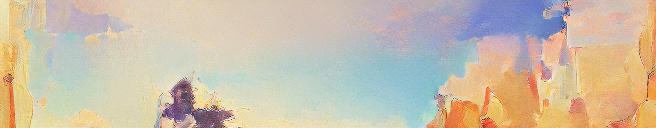Math and science::Algebra::Aluffi

Cosets

Coset

Let $G$ be a group and $H \subset G$ a subgroup.

For any $a \in G$ , a right-coset of $H$ is any set of the form:

H a

For any $a \in G,$ a left-coset of $H$ is any set of the form:

a H

Coset equivalence relation

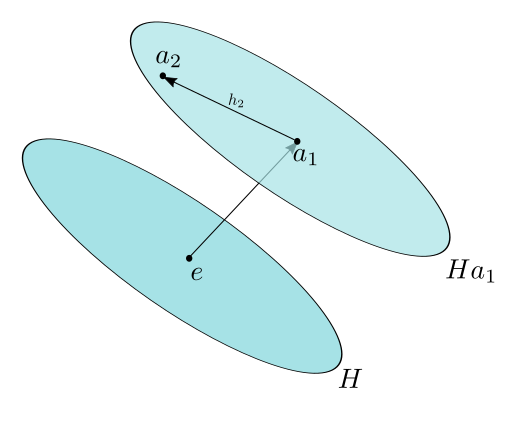
A right-coset forms a block in a partition defined by an equivalence relation, $\sim_{R}$ .

x \sim_{R} y ⟺ x y^{- 1} \in H

A left-coset forms a block in a partition defined by a equivalence relation, $\sim_{L}$ .

x \sim_{L} y ⟺ x^{- 1} y \in H

The essence of the relations is to consider an element related to another if the inverse of one element brings the other element back to $H$ .

The quotient group property

The equivalence relation above that defines a partition of right cosets satisfies an important property. An in fact, this property can define the equivalence relation, assuming a fixed subgroup $H$ . This property appears on the LHS below:

(\forall g \in G, x \sim y ⟹ x g \sim y g) ⟺ x y^{- 1} \in H ⟺ H a = H b

The property also asserts that $H$ is the equivalence class of $e_{G}$ .

$\sim_{R}$ is a valid equivalence relation

Shown for the right coset equivalence relation,

x \sim_{R} y ⟺ x y^{- 1} \in H .

We can show that the above relation is reflexive, symmetric and transitive.

We have $x x^{- 1} = e \in H$ , so $x \sim x$ .
If $x \sim y$ , then $x y^{- 1} \in H$ . Observe that $(x y^{- 1})^{- 1} = y x^{- 1}$ , and this element is in $H$ , as $H$ is closed under the group operation.
If $x \sim y$ and $y \sim z$ , then we have $x y^{- 1} \in H$ and $y z^{- 1} \in H$ . Concatenating through the group operation we have $x y^{- 1} y z^{- 1} = x z^{- 1}$ , and this term is in $H$ , again as $H$ is closed under the group operation.

The same line of reasoning also applies to $\sim_{L}$ .

The partitions of $\sim_{R}$

A block in the partition corresponding to $\sim_{R}$ can be expressed in terms of $H$ and a single term from the class.

Proof. Let $A$ be one of the equivalence classes. If we fix an element $a \in A$ , then any element $x \in A$ has the property that $x a^{- 1} = h$ , for some $h \in H$ . In other words, $x = h a$ . With $x$ being arbitrary, this property is enough to define $A$ : any element having this property is in $A$ , and any element in $A$ is $ \sim_{\text{equivalent} $ to $a$ and has this property.

The same line of reasoning also applies to $\sim_{L}$ . Thus, any subgroup $H$ of $G$ is associated with 2 partitions of $G$ .

Intuition #1

The idea is to consider any element of $a_{2} \in H a_{1}$ as being expressible as $h_{2} a$ for some $h_{2} \in H$ . We are breaking $a_{2}$ into two components $h_{2}$ and $a_{1}$ . With this, it is easy to see that $h_{2}$ can be reached by $a_{2} a^{- 1}$ .

Visualization

Alternative treatment

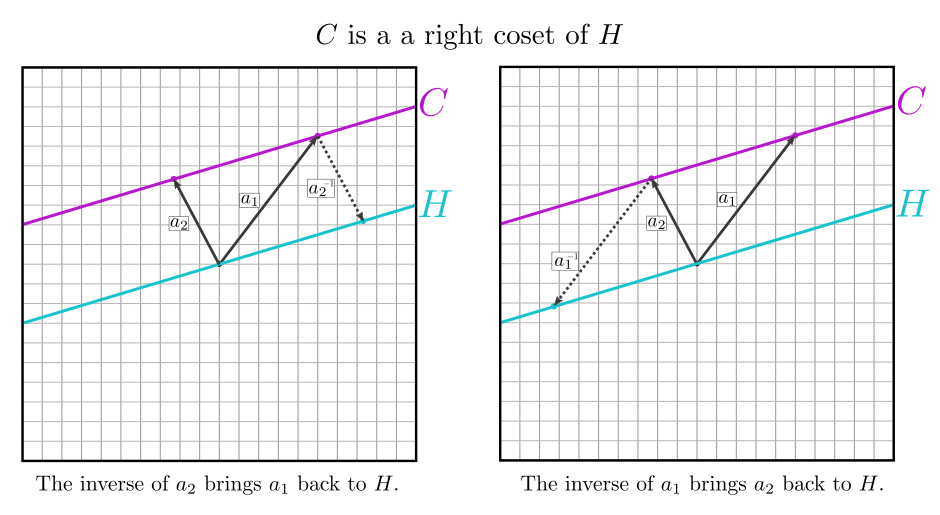
The material is presented in the reverse order in this intuitive post: https://math.stackexchange.com/a/1128688/52454.

Intuition

Intuition for why:

(\forall g \in G, x \sim y ⟹ x g \sim y g) ⟹ H a = H b

Consider $x = e_{G}$ . The equivalence class of $e_{G}$ maps to the subgroup $H$ . Now consider $g = a$ and then $g = b$ . For $g = a$ , we must have $\forall h \in H, h a \sim a$ . If this is not clear, note that $a \sim e_{G} \sim a$ , then apply the LHS of the implication above. Thus, all elements $H a$ are in an equivalence class. The same applies to $H b$ .

Now consider what happens if we assert that $a \sim b$ . As an equivalence relation is transitive, all elements $H a$ and $H b$ must also be equivalent.

A visualization of this idea is shown below.

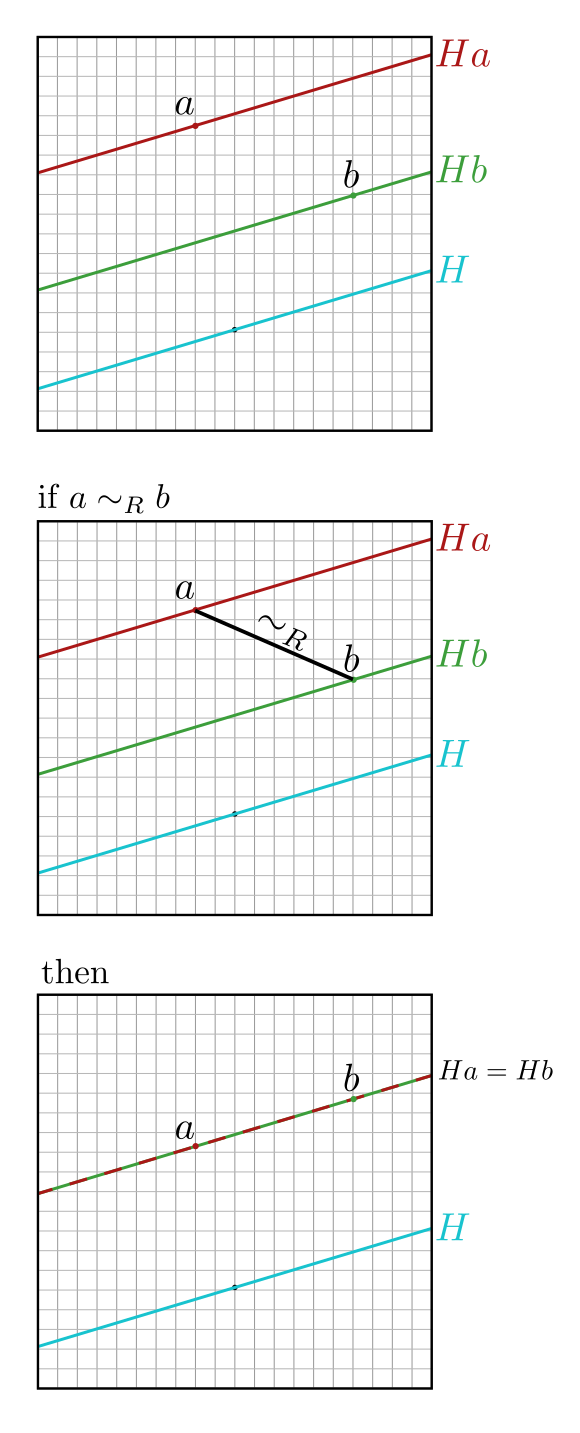
Not that this reasoning doesn't explain why $H a$ includes every element equivalent to $a$ . One must show why it's not possible for an element $v \in G$ to exist and for $v \sim a$ but $v \notin H a$ . To explain this, we note that $v \sim a$ implies that $v a^{- 1} \sim e_{G}$ , which in turn means that there exists some $h \in H$ such that $h a = v$ . Thus we have $v \in H a$ .

Source

https://math.stackexchange.com/questions/1128664/intuition-of-coset-of-a-subgroup

A good video on cosets: https://www.youtube.com/watch?v=IlFpiGhJ9cA&list=PLelIK3uylPMGzHBuR3hLMHrYfMqWWsmx5&index=5