\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \newcommand{\E} {\mathrm{E}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \newcommand{\groupMul}[1] { \cdot_{\small{#1}}} \newcommand{\inv}[1] {#1^{-1} } \)
Math and science::Algebra::Aluffi

Quotient group. From equivalence condition.

Under what conditions does an equivalence relation induce a quotient that is a group?

Quotient group

Let \( (G, \groupMul{G}) \) be a group. Let \( \sim \) be an equivalence relation on the set \( G \). Let \( \pi : G \to G / \!\sim \) be the quotient map induced by \( \sim \). Then \( (G/\!\sim, \groupMul{G/\!\sim}) \) is a group with operation:

\[ \pi(a) \groupMul{G/\!\sim} \pi(b) := \pi( a \groupMul{G} b) \]

iff \( \pi \) is a group homomorphism.

In turn, this is true of \( \pi \) iff:

\[ \begin{align} \forall a, a', g \in G, & \\ & a \sim a' \implies \quad ga \sim ga' \; \land \; ag \sim a'g \;. \end{align} \]

Background

The quotient of a set \( G \) with respect to an equivalence relation \( \sim \), expressed as \( G /\!\sim \), is simply the partition implied by \( \sim \).

Given a group \( (G, \groupMul{G}) \), it is natural to try and construct a group using the set \( G /\!\sim \) by inheriting the operation \( \groupMul{G} \) from \( G \). To be inheritable, \( \sim \) must meet a certain requirement. The essence of the requirement is that two elements of \( G \) that map to the same equivalence class should be treated alike in terms of \( \groupMul{G} \). This requirement is what is made precise in the above definition.

Relation to cosets

The right and left side of the condition:

\[ a \sim a' \implies ga \sim ga' \; \land \; ag \sim a'g \]

are satisfied by left and right cosets respectively, where the set in question, \( H \), is the equivalence class containing \( e_G \). In fact, each of these 2 conditions, when paired with a subgroup \( H \subset G \) is sufficient to define an equivalence relation on \( G \).

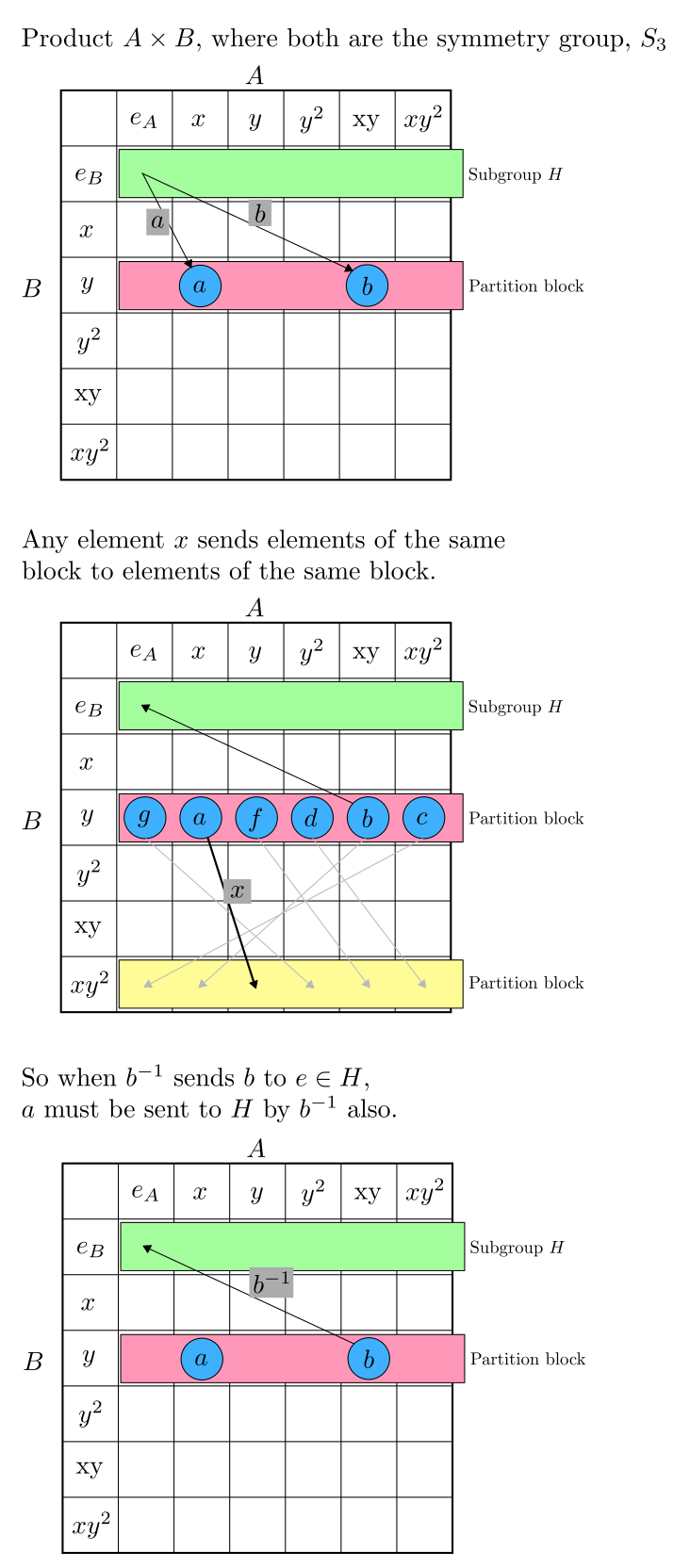
To see the connection, consider a right coset, \( Ha \), and consider two elements of the coset: the founding \( a \) and another arbitrary element, \( a' \in Ha \). Notice, by property of right cosets, that \( a' \) can be expressed as \( h_1a \) for same \( h_1 \in H \). So \( a'g = h_1ag \), but as \( h_1 \) is equivalent to \( e_G \), \( h_1ag \) must be in the same equivalence class as \( ag \).

Connection to the \( ab^{-1} \in H \) and \( a^{-1}b \in H \)

These two forms can be understood as expressing the fact that elements within an equivalence class act the same at the granularity of equivalences classes which is necessary for the quotient to be a group. Below is a visualization of this idea.

Alternative notation

The group operation is often defined compactly as:

\[ [a] \groupMul{G / \sim} [b] = [ab] \]

Source

Aluffi p90