Canonical decomposition in the Grp category
Theorem. Canonical decomposition in \( \cat{Grp} \)
In the \( \cat{Grp} \) catgeroy, every group homomorphism \( \varphi : G \to G' \) may be decomposed as follows:
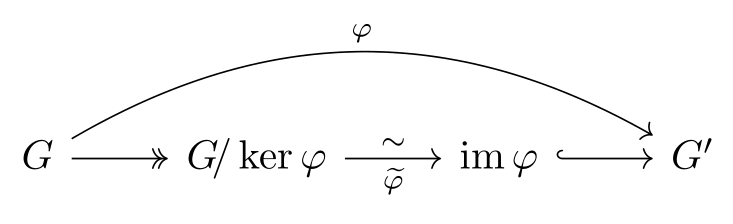
Where \( \widetilde{\varphi} \) is uniquely determined according to the universal property of quotient groups.
Analogous to the decomposition in \( \cat{Set} \)
The theorem is analogous to the decomposition of set functions (morphisms in \( \cat{Set} \) into a sequence of 3 maps: surjective map, bijective map then injective map.
Background propositions
The following propositions form the basis of the decomposition theorem.
normal \( \iff \) kernel
A subgroup is a normal subgroup iff it is a kernel of a group homomorphism.
We can make this statement as we know exactly which group homomorphism makes a normal subgroup a kernel. For a group \( G \), a normal subgroup \( H \) is one-to-one to a equivalence relationship \( \sim \) on \( G \) which permits the quotient \( G \!/ \sim \) to be a group. The map \( \pi : G \to G \!/ \sim \) sending elements to their equivalence class is a group homomorphism. Its identity is the coset \( e_GH \) and so its kernel is \( H \).
Normal subgroups define quotient groups
There is a group compatible equivalence relation iff there is a corresponding normal subgroup.
This is saying that for an equivalence relation \( \sim \) defined for a group \( (G, \groupMul{G}) \) which induces a quotient set \( G \!/\sim \), this quotient forms a group using \( \groupMul{G} \) iff the equivalence classes are the cosets of some subgroup \( H \) (with equal left and right cosets). This is what allows us to write \( G \!/H \) to represent a group.
The set quotient formed using \( H \) is special not only because it is a group, but because it satisfies a universal property analogous to the property that defines the quotient in the \( \cat{Set} \) category.
Quotient property in \( \cat{Grp} \)
Let \( G \) be a group. For any group homomorphism \( \varphi : G \to G' \), let \( H \subseteq \operatorname{ker} \varphi \) be the kernel of \( \varphi \), or any subgroup of it. Then there is a unique group homomorphism \( \widetilde{\varphi}: G \!/H \to G' \) so that the following diagram commutes: