Math and science::Analysis::Tao, measure::02. Lebesgue measure

Lebesgue outer measure (and Jordan inner measure) for any open set

Recall the result:

Let \( E \subset \mathbb{R}^d \) be expressible as the countable union of almost disjoint boxes, \( E = \bigcup_{n=1}^{\infty} B_n \). Then the Lebesgue outer measure of \( E \) is equal to the Jordan inner measure of \( E \). In other words:

\[ m^*(E) = m_{*,(J)}(E) = \lim_{N \to \infty} \sum_{n=1}^{N} |B_n| = \sum_{n=1}^{\infty} |B_n| \]

The leftmost equality is covered in Lemma 1.2.9. The next equality follows from \((\sum_{n=1}^{N}|B_n|)_{N} \) being a monotone increasing sequence, so the limit is also the supremum. There is no way to rearrange the sequence so that it doesn't converge, like having tiny boxes first (see Definition 8.2.1 in Tao Analysis I for a mention of this). The last equality is simply the definition of an infinite sum.

Theorem. Every open set can be expressed as a countable union of disjoint boxes.

So, the outer Lebesgue measure and Jordan inner measure of any open set \( E \) is the supremum of the volume of finite boxes filling the set. If we have a collection of boxes \( (B_n)_{n=1}^{\infty} \) that union to \( E \), then we can consider instead the limit of a sequence \( (\sum_{n=1}^{N})_N |B_n| \) where \( \bigcup_{n=1}^{\infty} B_n = E \).

We can't just consider any sequence boxes within \( E \), as you could union together a countable set of boxes that are too small to fill \( E \).

Dyadic mesh

A dyadic mesh is used for the proof of the theorem above. It is recalled here.

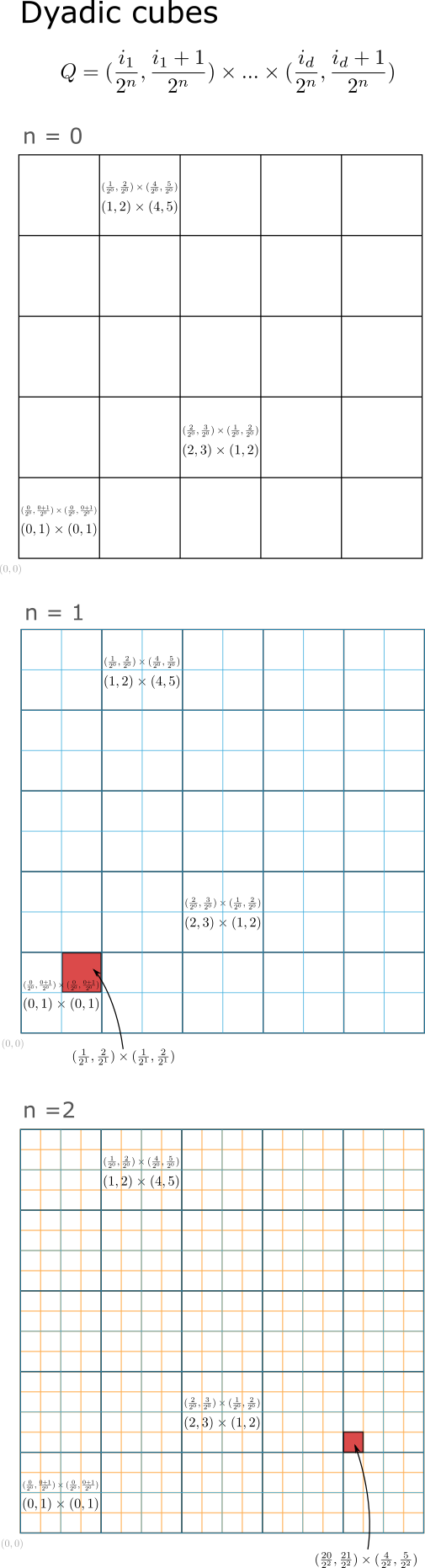
A dyadic mesh is a way of specifying cubes in \( \mathbb{R}^d \) such that \( \mathbb{R}^d \) is divided into disjoint cubes at multiple resolutions, and all boxes in a finer resolution combine to fit tightly into a a cube at the next level.

Countable and almost disjoint

The important magic of these dyadic cubes is that there is only countably many of them (across all resolutions!). So anything that can be represented as a set of dyadic cubes can be represented as a countable set of cubes. The formulaic organisation of the dyadic cubes allows for any set of them to be decomposed such that all dyadic cubes representing a set are all almost disjoint.

Countable disjoint dyadic cubes can represent any open set. Proof outline

Let \( E \subseteq \mathbb{R}^d \) be an open set. Consider a dyadic mesh where each cube \( Q \) is of the form:

\[ Q = [\frac{i_1}{2^n}, \frac{i_1 + 1}{2^n}] \times ... \times [\frac{i_d}{2^n}, \frac{i_d + 1}{2^n}] \]

Where the integer \( i \) specifies the coordinates of the cube and \( n \) the resolution level the cube exists in.

For every \( x \in E \) there must be an open ball centered at \( x \) (by the definition of open sets). Within an open ball centered at \( x \) we can find a closed dyadic cube containing \( x \) (how?). If we consider all \( x \in E \), we can construct a set \( \mathcal{S} \) of dyadic cubes that union to \( E \). As there are only countable dyadic cubes, \( \mathcal{S} \) is at most countable. Finally, the properties of dyadic cubes allows us to construct another set \( \mathcal{S}' \) of dyadic cubes such that all cubes are almost disjoint and \( \bigcup \mathcal{S} = \bigcup \mathcal{S}' = E \).

Source

p24