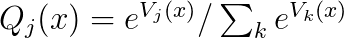\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \newcommand{\E} {\mathrm{E}} \)
deepdream of a sidewalk
Show Question
Softmax

The name "softmax" originates in contrast to the argmax function (considered a hard-max) which extracts the index of the element having the greatest value.

The argmax function with one-hot encoding:
\begin{displaymath} argmax(\begin{bmatrix}0.79 \\ 5.3 \\ -10.8 \end{bmatrix}) = \begin{bmatrix}0 \\ 1 \\ 0 \end{bmatrix} \end{displaymath} 

Compared to the softmax function:
\begin{gather*} softmax(\begin{bmatrix}0.79 \\ 5.3 \\ -10.8 \end{bmatrix}) = \begin{bmatrix} e^{0.79}/203 \\ e^{5.3}/203 \\ e^{-10.8}/203 \end{bmatrix} = \begin{bmatrix} 0.011 \\ 0.989 \\ 0.000 \end{bmatrix} (3df) \\ \text{Where } e^{0.79} + e^{5.3} + e^{-10.8} = 202.54 \end{gather*}

$e$ doesn't need to be the base and a more general form for the function is:
$e^{\beta x}$ where $\beta$ can be alterted to effectively change the base. It can be understood from this format how softmax approximates argmax. $\text{As } \beta \rightarrow \infty, \sigma(z) \rightarrow argmax(z)$

Benefits of softmax over argmax include:
* softmax is differentiable 
* softmax is continuous
* softmax is monotonic 
* softmax is positive for all inputs

Properties of softmax:
* invariant under translation. $\sigma(\vec{v} + \vec{c})_i = \frac{e^{\vec{z}_i + c}} {\sum_{k=1}^{k=|\vec{z}|}e^{\vec{z}_k + c}} = \frac{e^{\vec{z}_i} e^c} {\sum_{k=1}^{k=|\vec{z}|}e^{\vec{z}_k}e^{c}} = \sigma(\vec{v})$
* not invariant under scaling.

The sigmoid function is a special case of the softmax function. The sigmoid function is a softmax of 1D input in 2D space where one variable is kept as 0 (e.g. input is points along the x-axis in the (x,y) plane):
$sigmoid(x) = \frac{e^x}{e^0 + e^x} = \frac{e^x}{1 + e^x}$. Thus, the softmax activation function is said to generalize the sigmoid activation function to higher dimensions.

History
From Wikipedia:
In machine learning, the term "softmax" is credited to John S. Bridle in two 1989 conference papers, Bridle (1990a):[8] and Bridle (1990b):[3]

We are concerned with feed-forward non-linear networks (multi-layer perceptrons, or MLPs) with multiple outputs. We wish to treat the outputs of the network as probabilities of alternatives (e.g. pattern classes), conditioned on the inputs. We look for appropriate output non-linearities and for appropriate criteria for adaptation of the parameters of the network (e.g. weights). We explain two modifications: probability scoring, which is an alternative to squared error minimisation, and a normalised exponential (softmax) multi-input generalisation of the logistic non-linearity.[9] 

For any input, the outputs must all be positive and they must sum to unity. ...

Given a set of unconstrained values, $V_{j}(x)$, we can ensure both conditions by using a Normalised Exponential transformation:

        $Q_{j}(x)=e^{V_{j}(x)}/\sum _{k}e^{V_{k}(x)}$

This transformation can be considered a multi-input generalisation of the logistic, operating on the whole output layer. It preserves the rank order of its input values, and is a differentiable generalisation of the ‘winner-take-all’ operation of picking the maximum value. For this reason we like to refer to it as softmax.


Wikipedia has good coverage of the motivation of the softmax function.