\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \newcommand{\E} {\mathrm{E}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \newcommand{\groupMul}[1] { \cdot_{\small{#1}}} \newcommand{\inv}[1] {#1^{-1} } \)
Math and science::INF ML AI

Importance sampling

Let \( P(x) \) be a distribution which we can evaluate an unnormalized version easily at a point to obtain \( P^*(x) \). \( P(x) = \frac{P^*(x)}{Z} \) where \( Z = \int P^*(x) \dd{x} \). Now propose we have a function \( \phi(x) \) for which we wish to evaluate an expectation. We may proceed with uniform sampling by taking \( R \) samples of a uniform distribution over the domain, \( x_1, x_2, ... x_R \) and calculating an estimate:

\[ \mathrm{E}[\phi] = \frac{\sum_{i=1}^{R} P^*(x_i)\phi(x)}{\sum_{i=1}^{R} P^*(x_i)} \]

Importance sampling alters this calculation by sampling domain values from a distribution other than the uniform distribution. Let \( Q(x) \) be the sampler distribution. We will sample \( R \) samples from the sampler distribution and estimate the expectation of \( \phi \) like so:

todo

\[ \mathrm{E}[\phi] = \frac{} \]

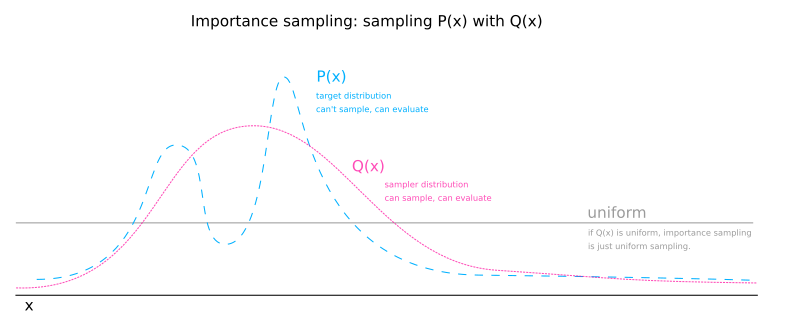
The sampler distribution has two effects:

  1. It focuses where in the domain \( x \) is sampled.
  2. It causes the estimation of the normalizing \( Z_P\) constant to be skewed by oversampling some values and undersampling others.

The first effect is beneficial and the second is not. The second effect can be conceptualised  as \( Q(x) \) stretching the domain in some places and shirking it in others. The size of the domain is important as a measure by which we are weighting the \( P^*(x) \) that we are collecting. To counteract the undesired effect of \( Q(x) \), we simply multiply \( P^*(x) \) by \( \frac{1}{Q(x) \). Any part of the domain that is stretch by \( Q(x) \) shrinks the weight given to a \( P^*(x) \) sample by multiplying by the reciprocal amount.

The fact that we multiply \( \phi(x) \) by \( P^*(x) \) fully accounts for the weighting for \( \phi \). The \( \frac{1}{Q(x_0) \) factor is simply to undo the fact that we are going to be sampling point \(x_0 \) excessively according to the value \( Q(x_0) \).


Efficient integration

Importance sampling is used in rendering. When performing integration, such as calculating the outgoing radiance by integrating incoming radiance, we are aware that light incidenct from the angle of the surface normal will have a large effect (cosine term near 1; the light flux is not stretched over the surface), while light hitting the surface from near perpendicular to the surface normal will have a small effect (cosine term near 0; light flux is spread over the surface). With this knowledge, it is wasteful to sample incident angles uniformly. Having high confidence of the contribution from glancing angles is wasteful as the effect from these angles on the overall sum is minuscule. Therefore, we wish to focus our sampling at the angles that will contribute more. This allows us to approach the true answer quicker with our estimate. Imagine a bell-shaped curve. The x value under the heavy bell center represents the light direction that will have a large impact, and the glancing angles are represented by the thin tails of the curve.

Source

Chapter 29, David MacKay