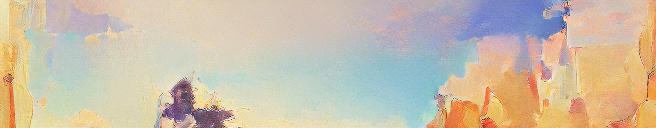\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \newcommand{\groupMul}[1] { \cdot_{\small{#1}}} \newcommand{\inv}[1] {#1^{-1} } \newcommand{\bm}[1] { \boldsymbol{#1} } \require{physics} \require{ams} \)

Cross-Entropy and KL divergence

Consider that we have an encoding scheme for sending codewords from a set \( C \) whose frequencies are given by the probability distribution \( q: C \to \mathbb{R} \). Assume that this scheme achieves the minimum average message length possible. The minimum possible average message length for any such encoding is equal to the entropy of the distribution, given by the equation:

Here, the syntax presents \( H \) as an operator taking in a distribution over \( C \).

Now, imagine that the same codewords are sent, but the frequency distribution of the codewords is changed to \( p: C \to \mathbb{R} \); the codewords are no longer optimized to the distribution. The new average length is given by the cross-entropy of [...] relative to [...]:

\( H_q(p) \) is also as an operator taking in a distribution over \( C \). Keeping this in mind helps remember the placement of \( q \) and \( p \) in the syntax \( H_q(p) \).

The length of a codeword is still the same ([what's the length of codeword \( x \in C \)?]) , but the probability of the codeword being sent/received has changed to \( p(x) \). The cross-entropy is always larger than the entropy of the original distribution. If we were to then update our encoding to a better \( p \)-optimized encoding, our average message length would decrease from \( H_q(p) \) to \( H(p) \).

KL divergence (a pseudo-difference measure between distributions)

Cross-entropy gives us a way to express how different two probability distributions are; the more different the distributions \( p \) and \( q \) are, the more the cross-entropy of \( q \) with respect to \( p \) will be bigger than the entropy of \( p \).

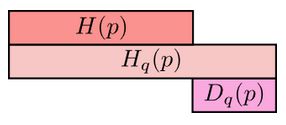
And the same goes for the cross-entropy of \( p \) with respect to \( q \):

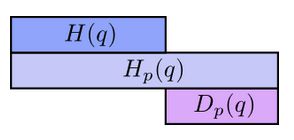
The differences, \( D_q(p) \) and \( D_p(q) \) are called Kullback-Leibler divergences (KL divergence). The KL divergence from [...] to [...], \( D_q(p) \) is defined as:

In words

The average message length reduction of using a \( q \)-optimized encoding when the transmission distribution is \( p \), then switching to a \( p \)-optimized encoding; this is the KL divergence from \( q \) to \( p \).